Timon Harz

December 16, 2024

Particle Swarm Optimization Explained: A Simple Guide for Beginners

Discover the power of Particle Swarm Optimization (PSO) in solving complex optimization tasks. This guide covers its principles, applications, and practical examples to get you started.

Particle Swarm Optimization (PSO) is a bio-inspired algorithm known for its simplicity in finding optimal solutions within a given solution space. Unlike other optimization techniques, PSO only requires the objective function and does not rely on gradients or any differential form of the objective. Additionally, it has very few hyperparameters to tune.

In this tutorial, you will discover the underlying principles of PSO and its algorithm through a practical example. By the end, you’ll understand:

What particle swarms are and how they behave under the PSO algorithm
The types of optimization problems PSO can solve
How to apply PSO to a real-world problem
The various variations of the PSO algorithm

Kickstart your project with my new book Optimization for Machine Learning, featuring step-by-step tutorials and Python source code for all examples.

Let’s dive in!

Particle Swarms

Particle Swarm Optimization was introduced by Kennedy and Eberhart in 1995. In their original paper, they drew inspiration from sociobiology, where groups of animals like schools of fish or flocks of birds benefit from the collective experience of the group. For example, when a bird searches for food, it may do so randomly, but by sharing its discoveries with the rest of the flock, the entire group benefits from improved hunting efficiency.

While we can simulate the movement of a flock of birds, we can also think of each bird as helping us search for the optimal solution within a high-dimensional solution space. The best solution found by the flock is considered the best solution in that space. This approach is heuristic, meaning that while we can never guarantee that the true global optimum will be found, the solutions discovered by PSO are often very close to it.

Example Optimization Problem

PSO is most effective for finding the maximum or minimum of a function defined in a multidimensional vector space. Imagine we have a function that outputs a real value based on a vector parameter, such as a coordinate in a plane. This function can take on almost any value in the space (for instance, the altitude at any point on the plane). By applying PSO, the algorithm will return the parameter that produces the minimum value of the function.

Let’s begin with the following example function:

f(x,y)=(x−3.14)2+(y−2.72)2+sin(3x+1.41)+sin(4y−1.73)

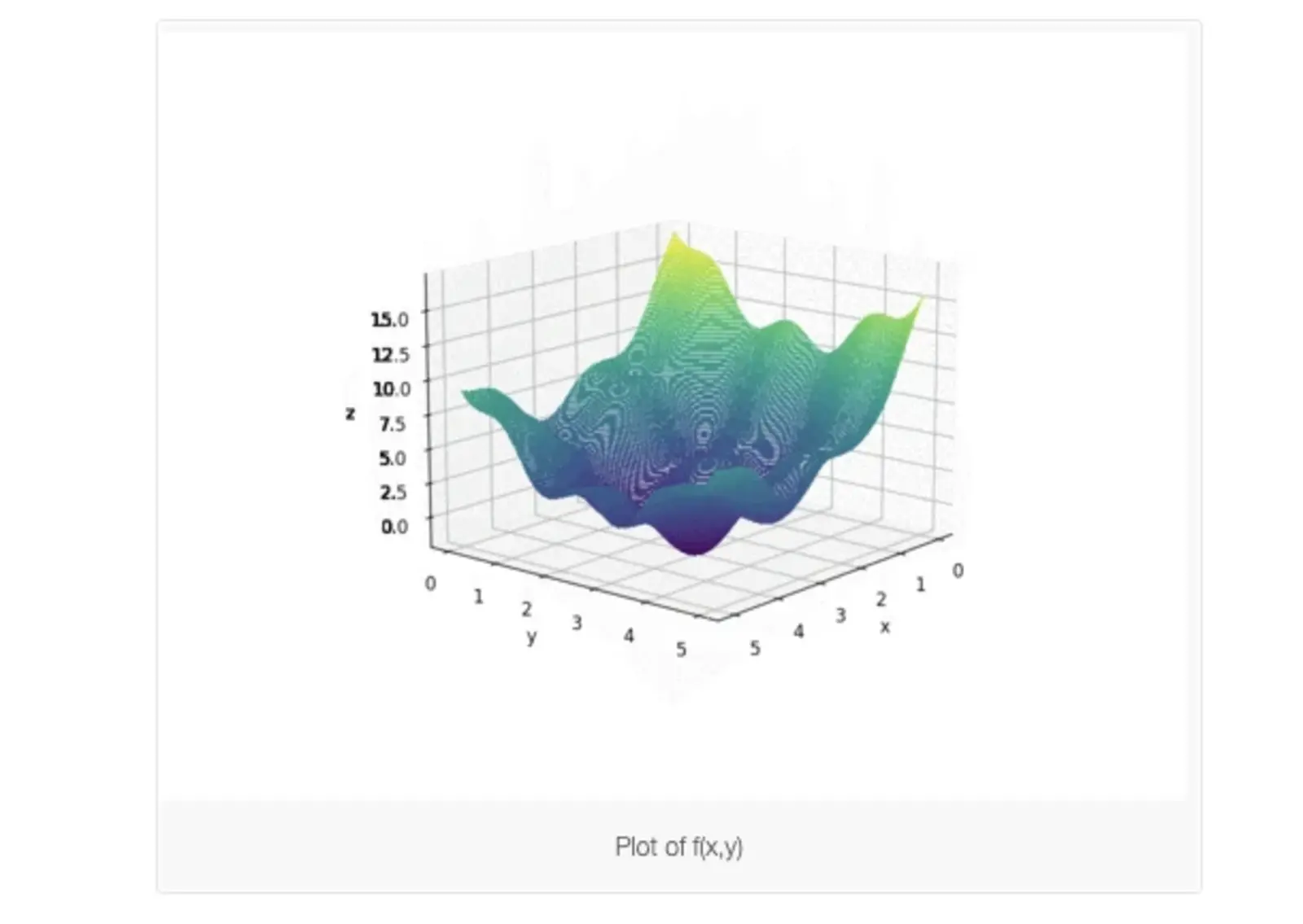
As shown in the plot above, this function resembles a curved egg carton. It is not convex, which makes finding its minimum challenging, as a local minimum does not necessarily represent the global minimum.

So, how can we find the minimum point of this function? One option is an exhaustive search—by evaluating the function at every point in the plane, we could pinpoint the minimum. Alternatively, we could randomly sample points on the plane and check which one yields the lowest value, though this may be too costly if we want to avoid searching every point. However, we can also observe from the shape of the function that once we find a point with a lower value, it becomes easier to find even smaller values nearby.

This is where particle swarm optimization comes in. Similar to how a flock of birds searches for food, we begin with several random points (particles) on the plane and let them search for the minimum in random directions. At each step, each particle explores around the best point it has found so far, as well as the best point found by the entire swarm. After a certain number of iterations, the minimum point found by the swarm is considered the best solution explored by the particles.

Algorithm Details

Assume we have P particles, and we denote the position of particle i at iteration t as X^i(t) = (x^i(t), y^i(t)). In the example above, this represents the particle’s coordinate. Along with the position, each particle also has a velocity, denoted as V^i(t) = (v^i_x(t), v^i_y(t)). At the next iteration, the position of each particle is updated as:

X^i(t+1) = X^i(t) + V^i(t+1)

Or equivalently:

x^i(t+1) = x^i(t) + v^i_x(t+1)

y^i(t+1) = y^i(t) + v^i_y(t+1)

At the same time, the velocities are updated using the following rule:

V^i(t+1) = wV^i(t) + c1 * r1 * (pbest^i - X^i(t)) + c2 * r2 * (gbest - X^i(t))

Where r1 and r2 are random numbers between 0 and 1, and w, c1, and c2 are constants specific to the PSO algorithm. pbest^i is the position that gives the best f(X) value ever explored by particle i, and gbest is the best position explored by all particles in the swarm.

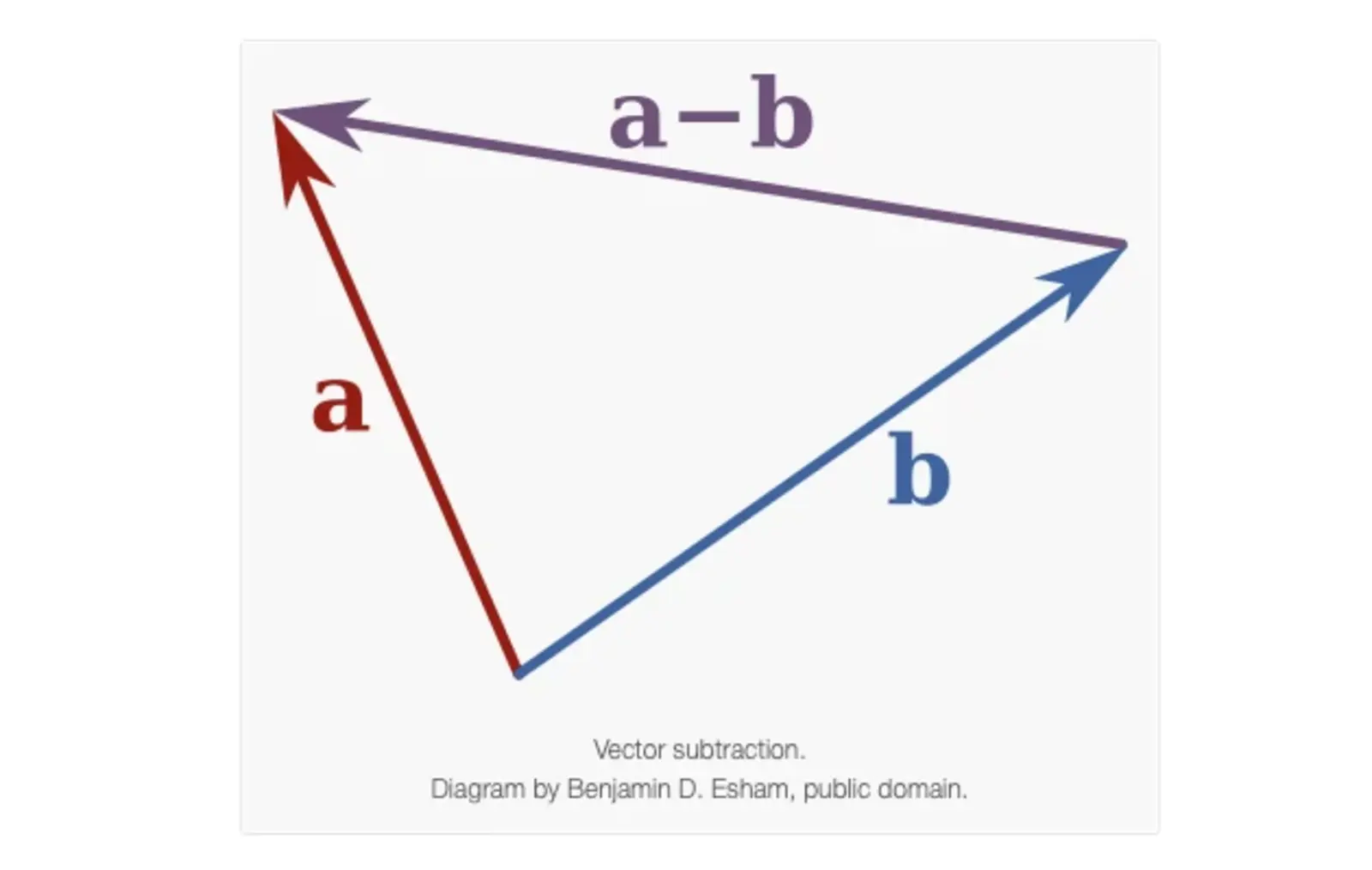
Note that pbest^i and X^i(t) are two position vectors, and the difference (pbest^i - X^i(t)) is a vector subtraction. The velocity update V^i(t) brings the particle back toward the position pbest^i.

We call the parameter "w" the inertia weight constant. It ranges from 0 to 1 and determines how much the particle should continue with its previous velocity (i.e., speed and direction of the search). The parameters c1 and c2 are called the cognitive and social coefficients, respectively. These parameters control how much weight is given to refining the search result of the particle itself and recognizing the search result of the entire swarm. We can consider these parameters to control the balance between exploration and exploitation.

The positions pbest^i and gbest are updated in each iteration to reflect the best positions ever found.

One unique property of this algorithm that sets it apart from other optimization algorithms is that it does not depend on the gradient of the objective function. In gradient descent, for example, we look for the minimum of a function f(X) by moving X to the direction of -∇f(X), as it is where the function goes down the fastest. For any particle at the position X at the moment, its movement does not depend on which direction is the "downhill" but only on where are pbest and gbest. This makes PSO particularly suitable for situations where differentiating f(X) is difficult.

Another property of PSO is its ability to be parallelized easily. As we manipulate multiple particles to find the optimal solution, each particle can be updated in parallel, and we only need to collect the updated value of gbest once per iteration. This makes the map-reduce architecture a perfect candidate for implementing PSO.

Implementation

Here we show how we can implement PSO to find the optimal solution.

For the same function as we showed above, we can first define it as a Python function and show it in a contour plot:

import numpy as np
import matplotlib.pyplot as plt
 
def f(x,y):
    "Objective function"
    return (x-3.14)**2 + (y-2.72)**2 + np.sin(3*x+1.41) + np.sin(4*y-1.73)
 
# Contour plot: With the global minimum showed as "X" on the plot
x, y = np.array(np.meshgrid(np.linspace(0,5,100), np.linspace(0,5,100)))
z = f(x, y)
x_min = x.ravel()[z.argmin()]
y_min = y.ravel()[z.argmin()]
plt.figure(figsize=(8,6))
plt.imshow(z, extent=[0, 5, 0, 5], origin='lower', cmap='viridis', alpha=0.5)
plt.colorbar()
plt.plot([x_min], [y_min], marker='x', markersize=5, color="white")
contours = plt.contour(x, y, z, 10, colors='black', alpha=0.4)
plt.clabel(contours, inline=True, fontsize=8, fmt="%.0f")
plt.show()

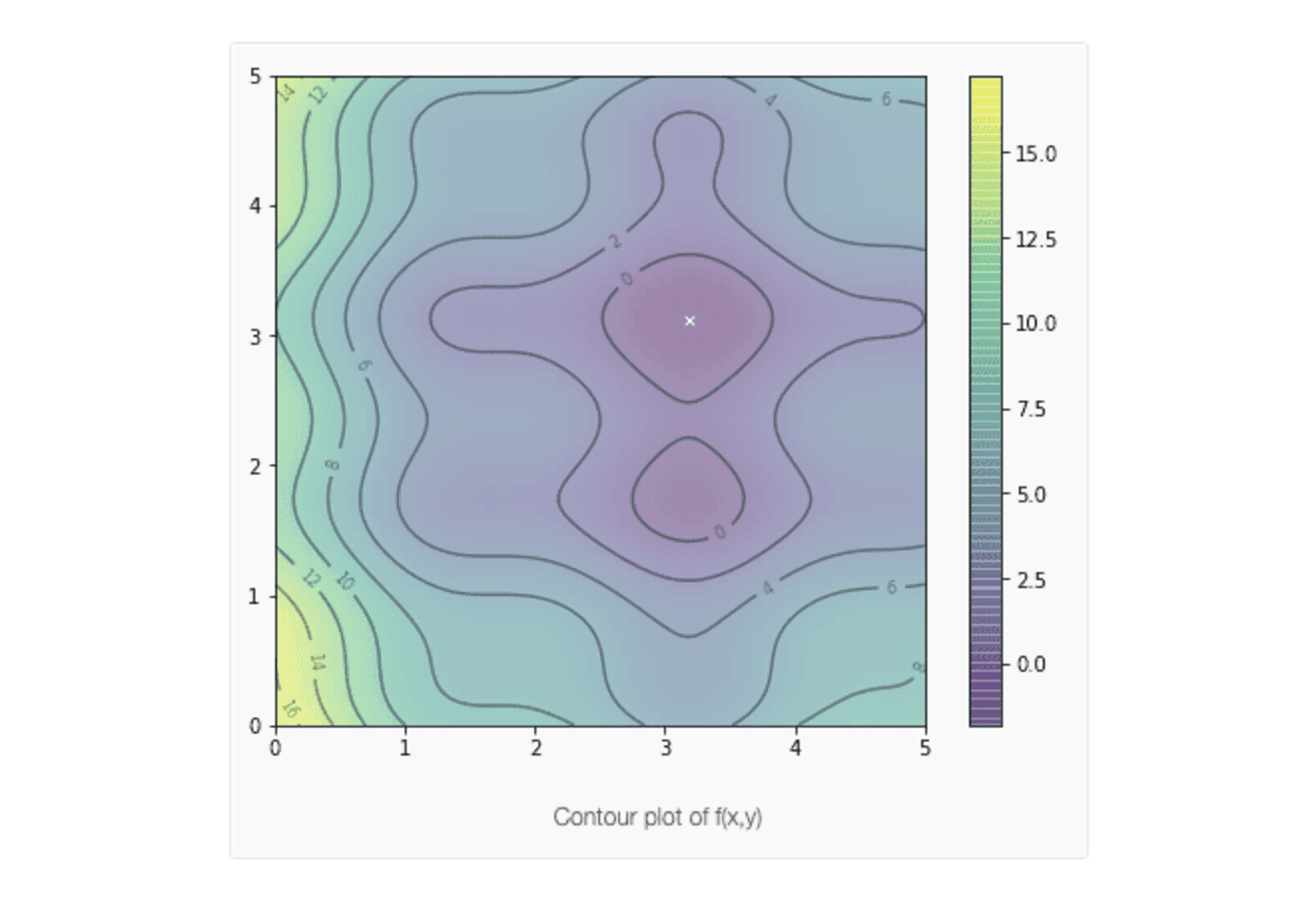
Here, we plot the function in the region where 0 < x, y < 5. We will generate 20 particles at random positions within this region, along with random velocities sampled from a normal distribution with a mean of 0 and a standard deviation of 0.1, as shown below:

n_particles = 20
X = np.random.rand(2, n_particles) * 5
V = np.random.randn(2, n_particles) * 0.1

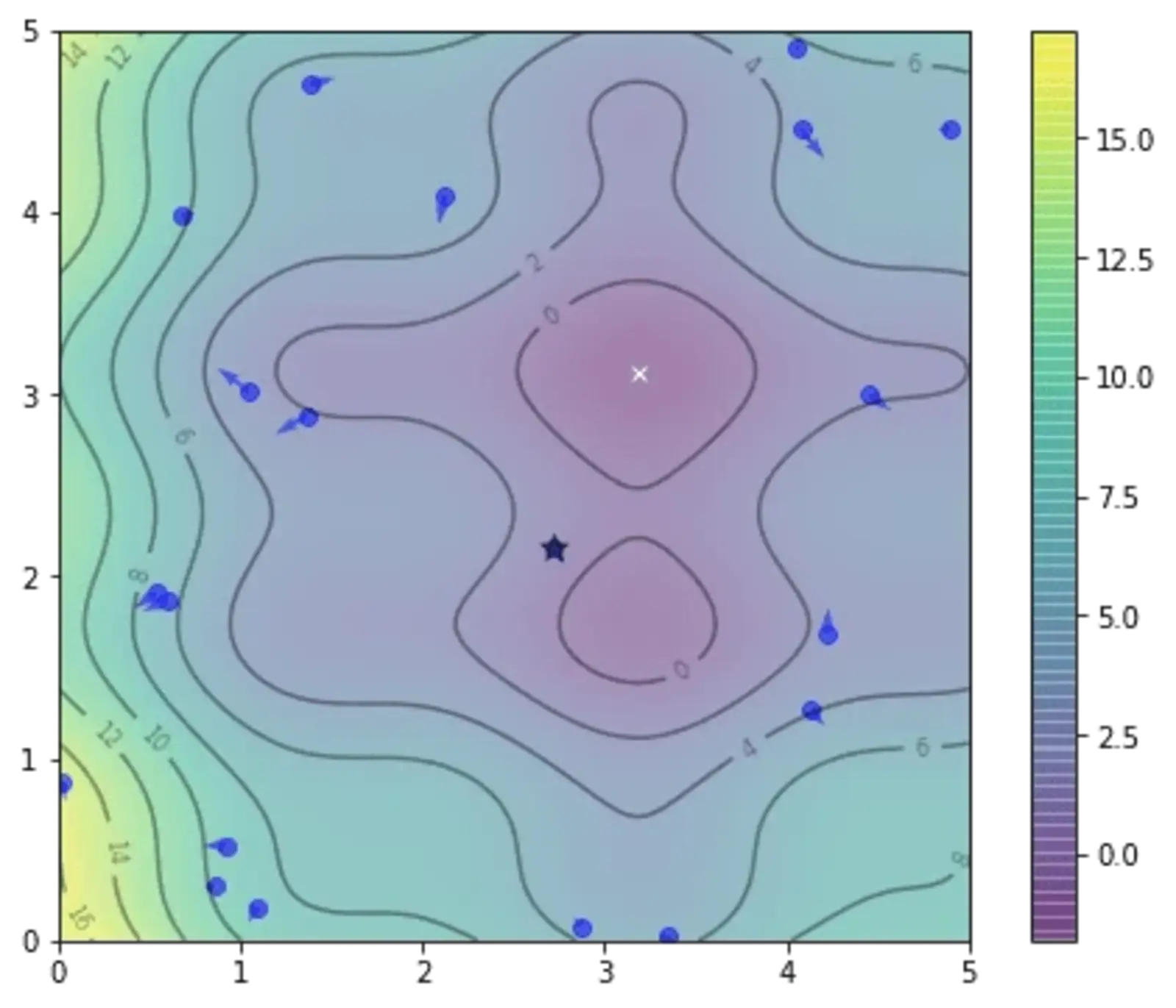
From this, we can determine the gbest as the best position found by all the particles so far. Since the particles haven't explored yet, their current position is also their pbest^i.

pbest = X
pbest_obj = f(X[0], X[1])
gbest = pbest[:, pbest_obj.argmin()]
gbest_obj = pbest_obj.min()

The vector pbest_obj represents the best value of the objective function found by each particle, while gbest_obj is the best value of the objective function ever found by the swarm. We use the min() and argmin() functions because this is a minimization problem. The position of gbest is indicated by a star below.

Let’s set c1= c2 = 0.1 and w = 0.8. Then we can update the positions and velocities according to the formula we mentioned above, and then update pbest^î and gbest afterwards:

c1 = c2 = 0.1
w = 0.8
# One iteration
r = np.random.rand(2)
V = w * V + c1*r[0]*(pbest - X) + c2*r[1]*(gbest.reshape(-1,1)-X)
X = X + V
obj = f(X[0], X[1])
pbest[:, (pbest_obj >= obj)] = X[:, (pbest_obj >= obj)]
pbest_obj = np.array([pbest_obj, obj]).max(axis=0)
gbest = pbest[:, pbest_obj.argmin()]
gbest_obj = pbest_obj.min()

The following shows the positions after the first iteration. The best position found by each particle is marked with a black dot, while their current positions are indicated in blue.

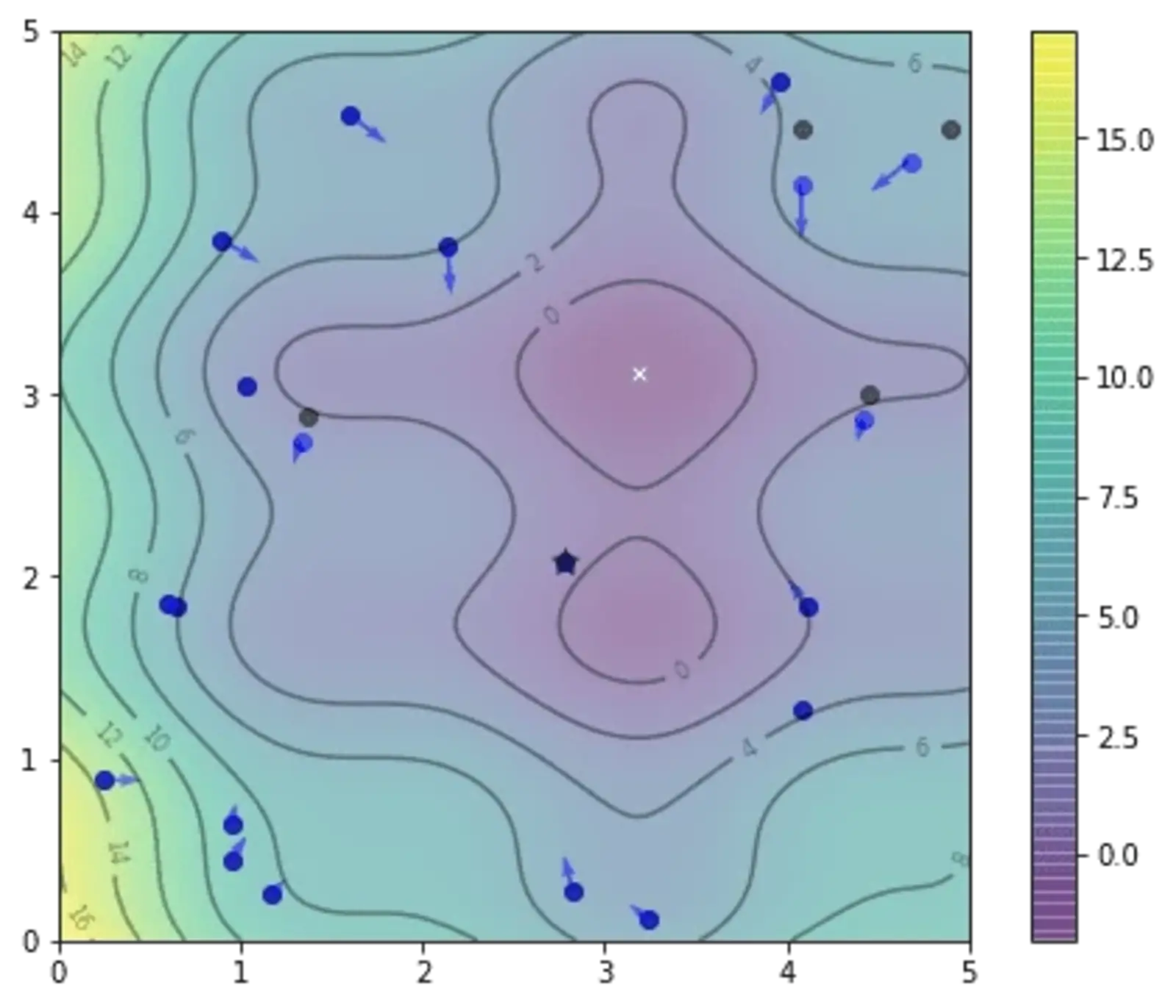
We can repeat the above code segment for multiple times and see how the particles explore. This is the result after the second iteration:

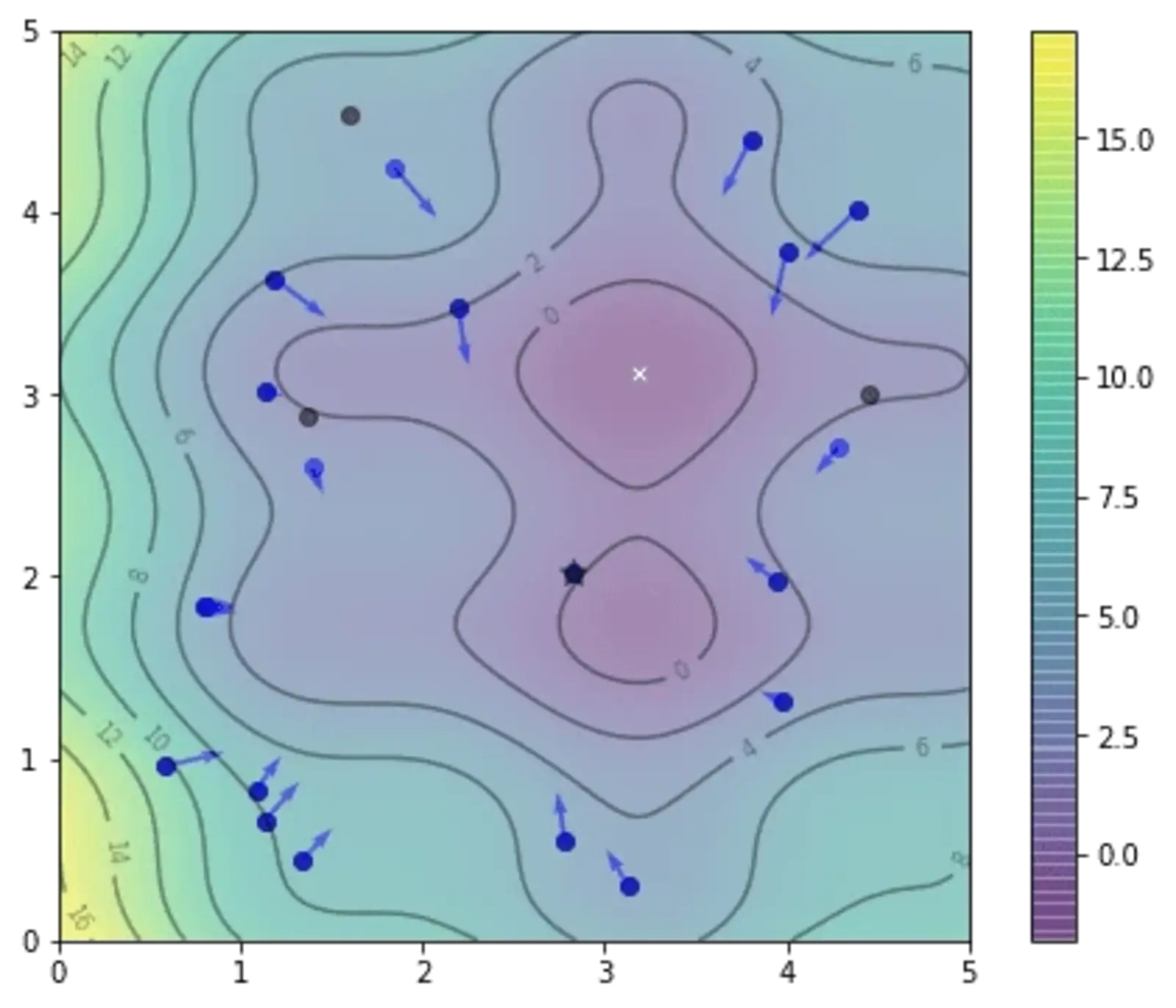
and this is after the 5th iteration, note that the position of gbest as denoted by the star changed:

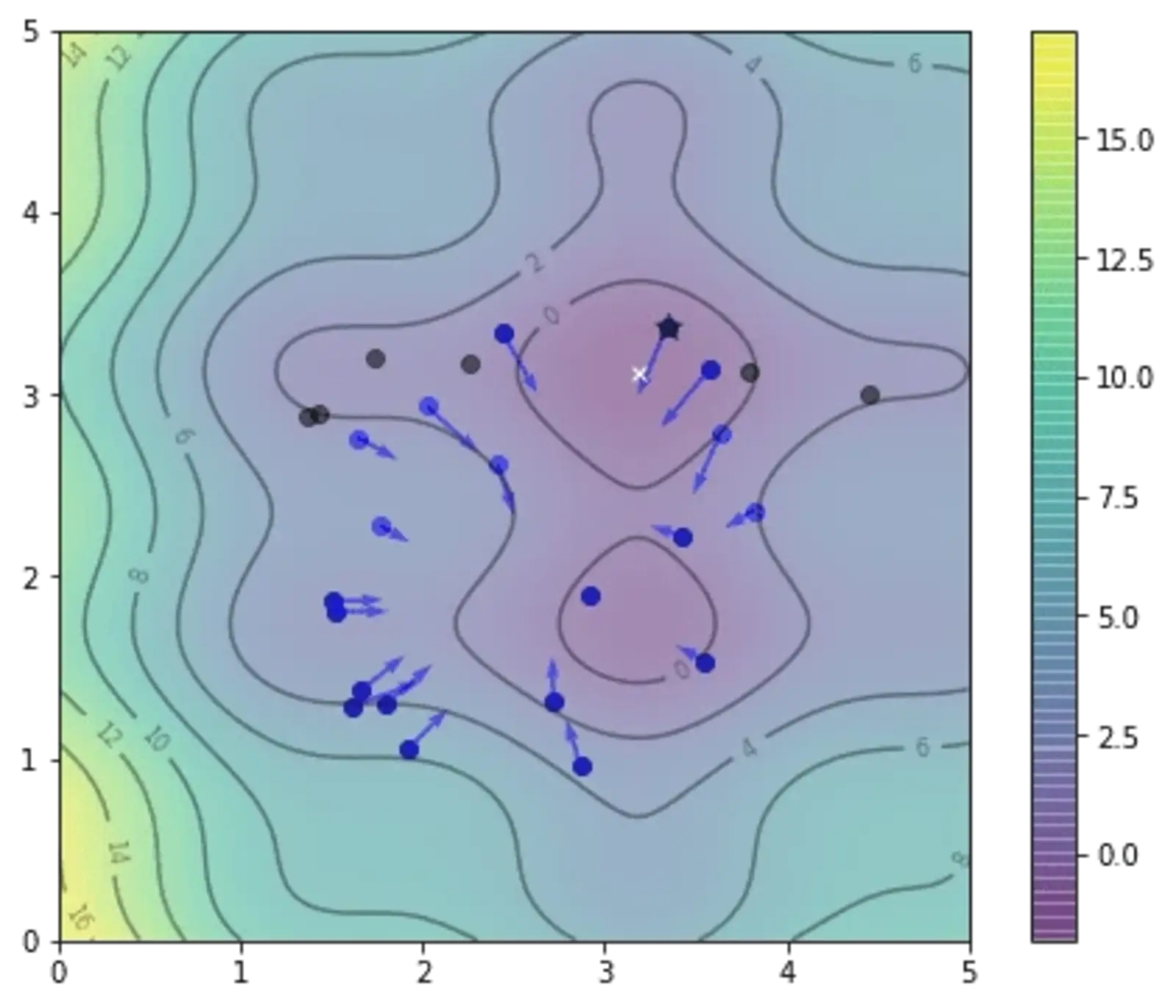
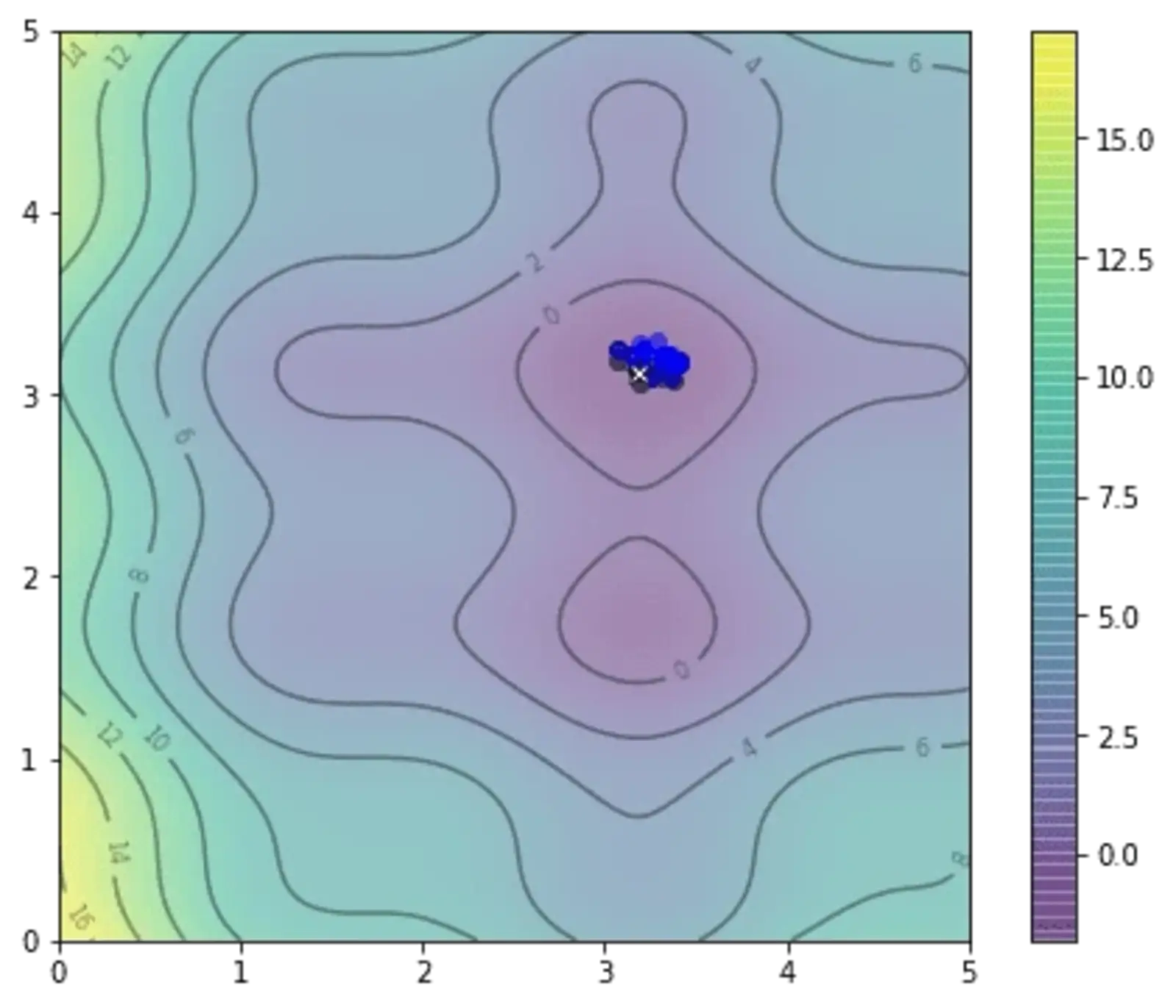
and after 20th iteration, we already very close to the optimal:

This is the animation showing how we find the optimal solution as the algorithm progressed. See if you may find some resemblance to the movement of a flock of birds:

So how close is our solution? In this particular example, the global minimum we found by exhaustive search is at the coordinate (3.182, 3.131) and the one found by PSO algorithm above is at (3.185, 3.130).

Variations

Most PSO algorithms are similar to the one described above. In the example provided, we set the PSO to run for a fixed number of iterations. However, it’s easy to modify the algorithm to adjust the number of iterations dynamically based on progress. For instance, we could stop the algorithm once the global best solution hasn’t improved over several iterations.

Research on PSO has largely focused on determining the optimal values for the hyperparameters (inertia weight, cognitive coefficient, and social coefficient) or varying these parameters as the algorithm progresses. One common approach is to make the inertia weight decrease linearly over time. Other proposals suggest reducing the cognitive coefficient while increasing the social coefficient to encourage more exploration early in the process and greater exploitation later on. For example, see the works of Shi and Eberhart (1998) and Eberhart and Shi (2000).

Complete Example

It’s straightforward to modify the above code to solve an objective function with more dimensions or switch from minimization to maximization. Below is the complete example of finding the minimum point of the previously proposed function, along with the code to generate the plot animation:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
 
def f(x,y):
    "Objective function"
    return (x-3.14)**2 + (y-2.72)**2 + np.sin(3*x+1.41) + np.sin(4*y-1.73)
    
# Compute and plot the function in 3D within [0,5]x[0,5]
x, y = np.array(np.meshgrid(np.linspace(0,5,100), np.linspace(0,5,100)))
z = f(x, y)
 
# Find the global minimum
x_min = x.ravel()[z.argmin()]
y_min = y.ravel()[z.argmin()]
 
# Hyper-parameter of the algorithm
c1 = c2 = 0.1
w = 0.8
 
# Create particles
n_particles = 20
np.random.seed(100)
X = np.random.rand(2, n_particles) * 5
V = np.random.randn(2, n_particles) * 0.1
 
# Initialize data
pbest = X
pbest_obj = f(X[0], X[1])
gbest = pbest[:, pbest_obj.argmin()]
gbest_obj = pbest_obj.min()
 
def update():
    "Function to do one iteration of particle swarm optimization"
    global V, X, pbest, pbest_obj, gbest, gbest_obj
    # Update params
    r1, r2 = np.random.rand(2)
    V = w * V + c1*r1*(pbest - X) + c2*r2*(gbest.reshape(-1,1)-X)
    X = X + V
    obj = f(X[0], X[1])
    pbest[:, (pbest_obj >= obj)] = X[:, (pbest_obj >= obj)]
    pbest_obj = np.array([pbest_obj, obj]).min(axis=0)
    gbest = pbest[:, pbest_obj.argmin()]
    gbest_obj = pbest_obj.min()
 
# Set up base figure: The contour map
fig, ax = plt.subplots(figsize=(8,6))
fig.set_tight_layout(True)
img = ax.imshow(z, extent=[0, 5, 0, 5], origin='lower', cmap='viridis', alpha=0.5)
fig.colorbar(img, ax=ax)
ax.plot([x_min], [y_min], marker='x', markersize=5, color="white")
contours = ax.contour(x, y, z, 10, colors='black', alpha=0.4)
ax.clabel(contours, inline=True, fontsize=8, fmt="%.0f")
pbest_plot = ax.scatter(pbest[0], pbest[1], marker='o', color='black', alpha=0.5)
p_plot = ax.scatter(X[0], X[1], marker='o', color='blue', alpha=0.5)
p_arrow = ax.quiver(X[0], X[1], V[0], V[1], color='blue', width=0.005, angles='xy', scale_units='xy', scale=1)
gbest_plot = plt.scatter([gbest[0]], [gbest[1]], marker='*', s=100, color='black', alpha=0.4)
ax.set_xlim([0,5])
ax.set_ylim([0,5])
 
def animate(i):
    "Steps of PSO: algorithm update and show in plot"
    title = 'Iteration {:02d}'.format(i)
    # Update params
    update()
    # Set picture
    ax.set_title(title)
    pbest_plot.set_offsets(pbest.T)
    p_plot.set_offsets(X.T)
    p_arrow.set_offsets(X.T)
    p_arrow.set_UVC(V[0], V[1])
    gbest_plot.set_offsets(gbest.reshape(1,-1))
    return ax, pbest_plot, p_plot, p_arrow, gbest_plot
 
anim = FuncAnimation(fig, animate, frames=list(range(1,50)), interval=500, blit=False, repeat=True)
anim.save("PSO.gif", dpi=120, writer="imagemagick")
 
print("PSO found best solution at f({})={}".format(gbest, gbest_obj))
print("Global optimal at f({})={}".format([x_min,y_min], f(x_min,y_min)))